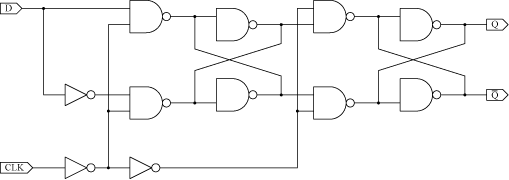
図1. Dフリップフロップの回路図
先週の実験では、Verilog を用いて組合せ回路を設計した。今週は順序回路の設計を学ぶ。
Dフリップフロップはクロック信号線が立ち上がった(0から1へ変化した)瞬間の入力D の値を記憶する記憶素子である。Dフリップフロップの回路図を図1に示す。

図1. Dフリップフロップの回路図
Verilog において Dフリップフロップを記述したいとき、この回路図をそのまま assign 文で記述してはいけない。Verilog においてフリップフロップは手続きブロックを用いて記述される。図2 に Dフロップフロップの記述例を示す。
module D_FLIPFLOP(D, CLK, Q);
input D;
input CLK;
output Q;
reg Q;
always@(posedge CLK) begin
Q <= D;
end
endmodule
|
図2. Dフリップフロップの Verilog記述
入力信号値が変化した瞬間に出力信号値が変化する組合せ回路においては always に続く @(〜)には * 印を記述した。一方、クロックが立ち上がった瞬間にのみ出力値が更新されるフリップフロップを記述するときは、@(〜)にはキーワード posedge とクロック信号名を記述する。
図2の回路をシミュレーション実験で動作検証する。"Initialize Timing and Clock Wizard" において Clock Information は図3 のように Single clock とし、クロック入力 CLK を指定すること。
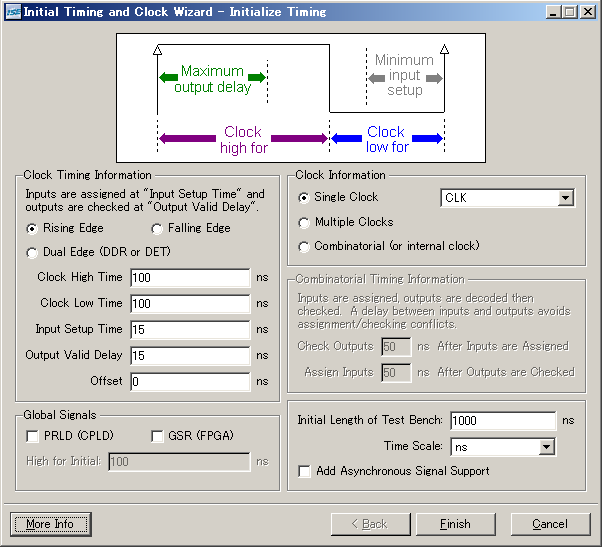
図3. クロックウィザードにおけるクロック入力の指定
図4に示すような波形エディタが起動する。クロック信号 CLK の波形は既にウィザードによって作成されているので入力信号 D だけ作成すればよい。
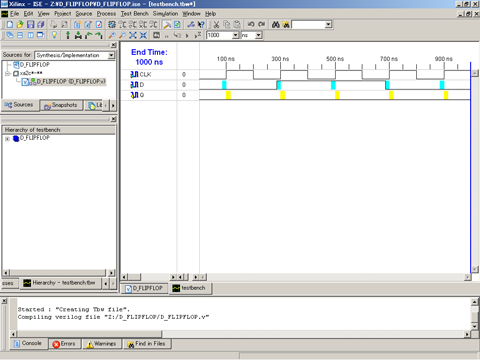
図4. クロック信号を有する回路に対する波形エディタ
図5にDフリップフロップに対するシミュレーション結果例を示す。クロックが立ち上がった瞬間に出力 Q の値が入力 D の値によって更新されている。シミュレーション開始直後から最初のクロック立ち上がり時まで、つまり0ns〜100nsにおいて、出力 Q の値がメッシュで表示されている。これは出力値 Q が不定値であることを意味しており、フリップフロップの値が初期化されていないことに起因している。
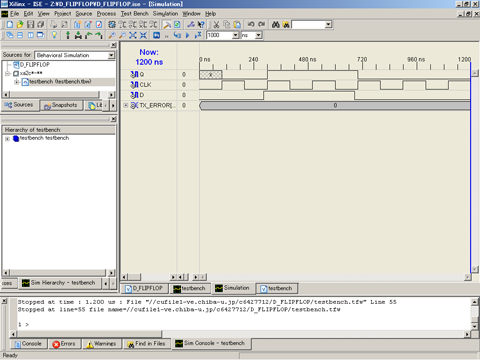
図5. Dフリップフロップのシミュレーション結果
先週の組合せ回路の場合と同様、手続きブロックの中には if, case などを用いた複雑な処理を書くことができる。図6は長さ4ビットのシフトレジスタの記述例である。リセット信号 RST が 1 のとき、シフトレジスタの値は全零にリセットされる。RST が 0 のとき、値がシフトする。ただし、値の更新はクロック入力 CLK が立ち上がった瞬間にのみ行われる。
module SHIFT_REGISTER(IN, CLK, RST, OUT);
input IN;
input CLK;
input RST;
output [3:0] OUT;
reg [3:0] OUT;
always@(posedge CLK) begin
if(RST) begin
OUT <= 4'b0000;
end else begin
OUT <= {OUT[2:0], IN};
end
end
endmodule
|
図6. 4ビットシフトレジスタの Verilog記述
リセット信号付き 5進カウンタを Verilog で記述せよ。
次に、16点離散フーリエ変換演算回路を題材に複雑な順序回路設計を行う。フーリエ変換とは波情報の時間領域から周波数領域への変換であり、音声処理、画像処理など、さまざまな情報の処理にしばしば用いられる。16点離散フーリエ変換は離散化された要素数16の数列に対するフーリエ変換である。16点離散フーリエ変換演算Excelファイルを用意したので、これを用いてフーリエ変換について思い出して欲しい。
16点離散フーリエ変換の回路図を図7に示す。
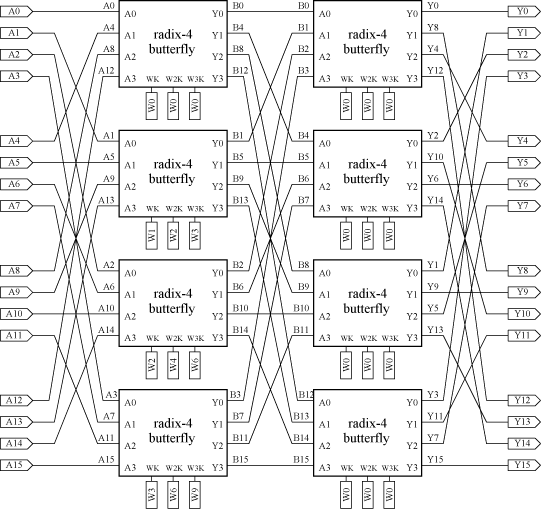
図7. 16点離散フーリエ変換のデータフロー
この回路の各信号線はバスであり、それぞれ複素数を扱う。入力として時間領域の波情報 A0〜A15、出力として周波数領域の情報 Y0〜Y15 を持つ。16点離散フーリエ変換では回転因子 W16 (以下、簡単に W) およびそのべき乗値 Wk が用いられる。これは次式で得られる。
![]()
この式は三角関数を含む。三角関数演算回路の構成は難しい。しかし幸い、この式の値は k によってのみ定まり、また、この回路においては k は 0, 1, 2, 3, 4, 5, 6, 9 以外の値をとらない。よって、Wkの値は事前に計算しておき、回路に保持させることにする。図7 では W0〜W9 にこれらの定数値が保持されている。
図7中の "radix-4 butterfly" は基数4のバタフライ演算回路であり、図8のように構成できる。
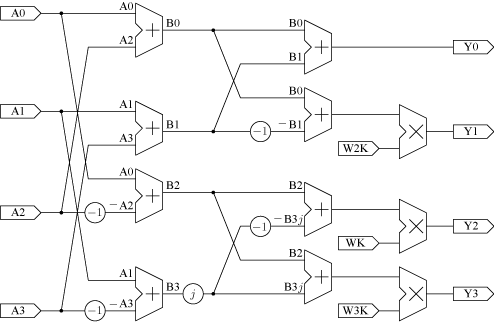

図8. 基数4のバタフライ演算回路
この回路において、データはすべて 32ビットバスで扱うこととし、上位 16ビットを実数部、下位 16ビットを虚数部とみなすことにする。扱う数値は2の補数表現による整数値のみである。原則、小数点以下の値は切り捨てる。ただ、Wk については小数点以下を無視することはできない。そこで、Wk は乗算器の1入力にしかならないことに注目し、Wk の代わりに Wk を 214倍した値を用いることとし、乗算器の出力において、積を 214で割る (下位14ビットを捨てる) こととする。16進表記した 214Wk を、表1に示す。また簡単のため、加減乗算器でオーバフローは起きないと仮定する。
表1. 214Wk (16進表記)
| 実数部 | 虚数部 | |
|---|---|---|
| W0 | 4000 | 0000 |
| W1 | 3b21 | e782 |
| W2 | 2d41 | d2bf |
| W3 | 187e | c4df |
| W4 | 0000 | c000 |
| W5 | e782 | c4df |
| W6 | d2bf | d2bf |
| W9 | c4df | 187e |
図7 の 16点離散フーリエ変換演算回路(組合せ回路)を Verilog で設計せよ。
図7 の 16点離散フーリエ変換演算回路について、適宜フリップフロップを挿入し、入力とフリップフロップ間とフリップフロップ同士の間、フリップフロップと出力間に入るバタフライ演算回路の数を高々1個に制限せよ。
図7 ではデータ入力出力それぞれについて、それぞれ16個のポート A0〜A15, Y0〜Y15 を設けている。これをそれぞれ1個に減らした16点離散フーリエ変換演算回路を作成せよ。具体的に図9 のように入出力 A, Y を設け、16個のデータ A0〜A15, Y0〜Y15 を逐次入出力できるようにせよ。ここで、入力 START を設け、データ入力開始を回路に知らせることができるようにすると共に、データ出力の開始を回路が示せるように出力 DONE を設けよ。
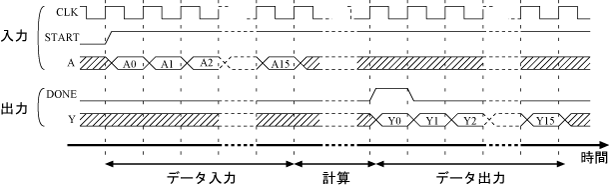
図9. 逐次入出力16点離散フーリエ変換のタイムチャート
その他、自由に改良を加えよ。
難波 一輝 (助教・伊藤・北神・難波研究室)
工学部1号棟4階409号室、内線3255、043-290-3255、namba@ieee.org