情報画像学実験II
実験II-1. 論理回路
回路作成例・解説
第3週目-課題1
第2週目の図1, 第3週目の図10 をそのまま Verilog で記述すれば図1, 2 のようになる。
module HALF_ADDER(A, B, S, CO);
input A;
input B;
output S;
output CO;
assign CO = A & B;
assign S = (A | B) & ~CO;
endmodule
|
図1. 半加算器の Verilog 記述例
module FULL_ADDER(A, B, CI, S, CO);
input A;
input B;
input CI;
output S;
output CO;
wire U1_S;
wire U1_CO;
wire U2_CO;
HALF_ADDER U1 (.A(A), .B(B), .S(U1_S), .CO(U1_CO));
HALF_ADDER U2 (.A(U1_S), .B(CI), .S(S), .CO(U2_CO));
assign CO = U1_CO | U2_CO;
endmodule
|
図2. 全加算器の Verilog 記述例
第3週目-課題2A
4ビット加減算器の回路図と Verilog 記述例を図3, 4 に示す。
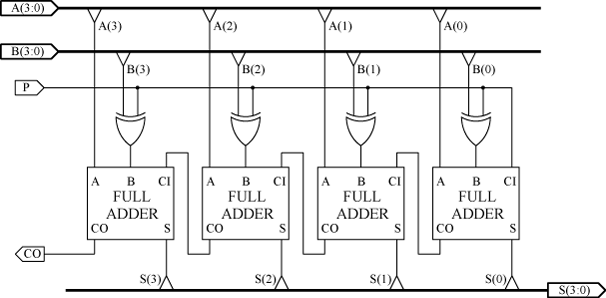
図3. 4ビット加減算器の回路図
module ADDER_SUBTRACTOR(A, B, S, CO, P);
input [3:0] A;
input [3:0] B;
input P;
output [3:0] S;
output CO;
wire [3:0] BX;
wire U0_CO;
wire U1_CO;
wire U2_CO;
assign BX = B ^ {4{P}}; // BX[i] = B[i] ^ P (0≦i<4)
FULL_ADDER U0 (.A(A[0]), .B(BX[0]), .CI(P), .S(S[0]), .CO(U0_CO));
FULL_ADDER U1 (.A(A[1]), .B(BX[1]), .CI(U0_CO), .S(S[1]), .CO(U1_CO));
FULL_ADDER U2 (.A(A[2]), .B(BX[2]), .CI(U1_CO), .S(S[2]), .CO(U2_CO));
FULL_ADDER U3 (.A(A[3]), .B(BX[3]), .CI(U2_CO), .S(S[3]), .CO(CO));
endmodule
|
図4. 4ビット加減算器の Verilog 記述例
第3週目-課題2B
2進数表記した2値に対する筆算による乗算例を図5に示す。
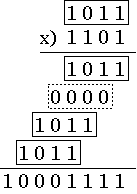
図5. 乗算例
例の場合は、乗数の第3, 2, 0 ビットが 1、第1ビットが 0 であり、被乗数1011 を 3, 2, 0 ビット左シフトして得られる3値の和を取ることにより積を得ることができる。一般に、乗数の各ビットの値を調べ、1となるすべてのビット(第iビットとする)について、被乗数をiビット左シフトして得られる値を求め、それぞれの和を取ることにより、積を得ることができる。ここで、図6 に示すようにバスAの各値と乗数の iビット目の値 B[i] の論理積(AND)演算により、B[i] が 1 であるとき被乗数 A、0であるとき全零になるバス ABi を得ることができる。
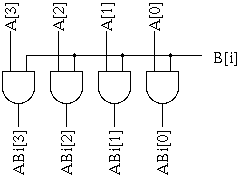
図6. ABi (i=0〜3) を求める回路
積YはABi (i=0〜3) をiビット左シフトして得られる値の総和をとることにより得られる。左シフト操作には特殊な回路を用いる必要はなく、配線を左にずらすことで実現できる。積Yは8ビット値で得られる。一般に積の桁数は、高々、被乗数と乗数の桁数の和である。この場合は被乗数と乗数の桁数は共に高々4桁であり、積の桁数も高々4+4=8桁となる。図7 に4ビット乗算器の構成を示す。なお、図7には含めていないが4ビット乗算器には ABi を求めるための図6に示す回路が4個必要である。
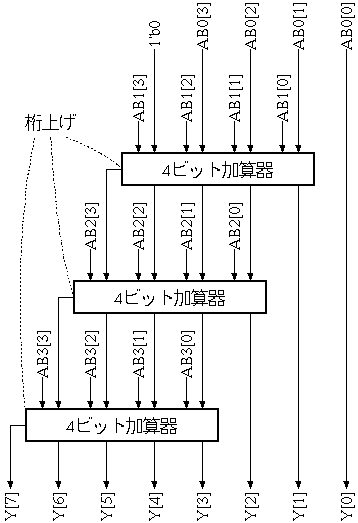
図7. 4ビット乗算器
図7に基づいて作成した4ビット乗算器 Verilog 記述例を以下に示す。モジュール ADDER4 は課題1で作成した4ビット加算器である。また、モジュール MULTIPLIER4X1 は図6に示す ABi を求める回路である。モジュール MULTIPLIER4X1 の記述例を図8に示す。
module MULTIPLIER4(A, B, Y);
input [3:0] A;
input [3:0] B;
output [7:0] Y;
wire [3:0] AB3;
wire [3:0] AB2;
wire [3:0] AB1;
wire [3:0] AB0;
wire [3:0] U4_S;
wire [3:0] U5_S;
wire U4_CO;
wire U5_CO;
MULTIPLIER4X1 U0 (.A(A), .B(B[0]), .Y(AB0));
MULTIPLIER4X1 U1 (.A(A), .B(B[1]), .Y(AB1));
MULTIPLIER4X1 U2 (.A(A), .B(B[2]), .Y(AB2));
MULTIPLIER4X1 U3 (.A(A), .B(B[3]), .Y(AB3));
assign Y[0] = AB0[0];
ADDER4 U4 (.A({1'b0, AB0[3:1]}), .B(AB1), .S(U4_S), .CO(U4_CO));
assign Y[1] = U4_S[0];
ADDER4 U5 (.A({U4_CO, U4_S[3:1]}), .B(AB2), .S(U5_S), .CO(U5_CO));
assign Y[2] = U5_S[0];
ADDER4 U6 (.A({U5_CO, U5_S[3:1]}), .B(AB3), .S(Y[6:3]), .CO(Y[7]));
endmodule
|
図7. 4ビット乗算器の Verilog 記述例
module MULTIPLIER4X1(A, B, Y);
input [3:0] A;
input B;
output [3:0] Y;
assign Y = A & {4{B}};
endmodule
|
図8. ABiを求める回路の Verilog 記述例
この乗算器は加算器を3個持つ。一般に乗算器は加算器と比べ回路量がとても大きい。
ここで説明した乗算器では入出力値を符号なしの値として扱っている。課題4で説明するように、2の補数表現した符号付きの値を扱う乗算器は符号なし乗算器とは異なる構成の回路になり、また複雑である。ここでは説明しない。
第3週目-課題3
課題のページで示したセレクタの例のようにcase 文を用いることにより、真理値表をほぼそのままプログラムに書くことができる。先週分の解説に示した真理値表より、7セグメントデコーダは図9のように書ける。図9 では default 文において A〜G に 1'bx を代入している。x は不定値を意味する。0 になっても 1 になってもよい場合には不定値の代入を明記することが強く求められる。
module DECODER7(I3, I2, I1, I0, A, B, C, D, E, F, G);
input I3;
input I2;
input I1;
input I0;
output A;
output B;
output C;
output D;
output E;
output F;
output G;
reg A;
reg B;
reg C;
reg D;
reg E;
reg F;
reg G;
always @(*) begin
case({I3, I2, I1, I0})
// I3×8+I2×4+I1×2+I0 の値によって分岐
0: begin
A <= 0;
B <= 0;
C <= 0;
D <= 0;
E <= 0;
F <= 0;
G <= 1;
end
1: begin
A <= 1;
B <= 0;
C <= 0;
D <= 1;
E <= 1;
F <= 1;
G <= 1;
end
2: begin
A <= 0;
B <= 0;
C <= 1;
D <= 0;
E <= 0;
F <= 1;
G <= 0;
end
3: begin
A <= 0;
B <= 0;
C <= 0;
D <= 0;
E <= 1;
F <= 1;
G <= 0;
end
4: begin
A <= 1;
B <= 0;
C <= 0;
D <= 1;
E <= 1;
F <= 0;
G <= 0;
end
5: begin
A <= 0;
B <= 1;
C <= 0;
D <= 0;
E <= 1;
F <= 0;
G <= 0;
end
6: begin
A <= 0;
B <= 1;
C <= 0;
D <= 0;
E <= 0;
F <= 0;
G <= 0;
end
7: begin
A <= 0;
B <= 0;
C <= 0;
D <= 1;
E <= 1;
F <= 1;
G <= 1;
end
8: begin
A <= 0;
B <= 0;
C <= 0;
D <= 0;
E <= 0;
F <= 0;
G <= 0;
end
9: begin
A <= 0;
B <= 0;
C <= 0;
D <= 0;
E <= 1;
F <= 0;
G <= 0;
end
default: begin
// I3〜I0 が 10以上のとき
// つまり、サポート外の値が入力されたとき
A <= 1'bx; // x は不定値
B <= 1'bx; // つまり 0 でも 1 でも
C <= 1'bx; // どちらでもよい値
D <= 1'bx;
E <= 1'bx;
F <= 1'bx;
G <= 1'bx;
end
endcase
end
endmodule
|
図9. 手続きブロックを用いた7セグメントレジスタデコーダの Verilog 記述例
第3週目-課題4
例えば、(0001)2=1 と (1111)2=15 または -1 を例に考える。このとき、積は表1の通りになる。
表1. (0001)2 と (1111)2 の乗算結果
| 被乗数 | 乗数 | signed あり | signed なし
|
|---|
| 0001 | 0001 | 00000001(=1) | 00000001(=1)
|
| 0001 | 1111 | 11111111(=-1) | 00001111(=15)
|
| 1111 | 1111 | 00000001(=1) | 11100001(=225)
|
signed ありとなしのときでは2進数表記でも結果が異なることに注意されたい。2の補数表現を用いれば、正負の符号を気にせず加減算器を構成することができると習ったであろう。これは情報数学の妙の一つである。しかし、この妙も加減算器に限定した話である。乗算など他の演算を考えるときはやはり符号を気にする必要がある。
第2週目の回路作成例・解説に戻る
第4週目の回路作成例・解説に進む
実験II-1トップページに戻る
難波担当実験・演習のページに戻る
難波 一輝 (助教・伊藤・北神・難波研究室)
工学部1号棟4階409号室、内線3255、043-290-3255、namba@ieee.org



