課題図1の回路をそのまま verilog-HDL で記述すれば以下のようになる。
module MULTIPLEXER(A, B, C, Y);
input A, B, C;
output Y;
assign Y = A & ~C | B & C;
endmodule
|
真理値表は以下の通りとなる。
| 表1 マルチプレクサの真理値表 | ||||||||||||||||||||||||||||||||||||
|
この回路はC=0のときAの値を、C=1のときBの値を出力するセレクタ回路である。
マルチプレクサとはデジタル信号処理における圧縮機の一種であり、その構成の一部として、このセレクタ回路が用いられる。ただ、マルチプレクサと言ったとき、この課題のように、単にセレクタ回路を指すことも多い。
検証用モジュールの記述例を以下に示す。
`timescale 10ps / 10ps
module TESTBENCH;
reg A, B, C;
wire Y;
MULTIPLEXER CUT (.A(A), .B(B), .C(C), .Y(Y));
initial begin
$dumpfile("MULTIPLEXER.vcd");
$dumpvars(1, TESTBENCH);
C <= 0; A <= 0; B <= 0; #50
B <= 1; #50
A <= 1; B <= 0; #50
B <= 1; #50
C <= 1; A <= 0; B <= 0; #50
B <= 1; #50
A <= 1; B <= 0; #50
B <= 1; #50
$finish;
end
endmodule
|
記述例を以下に示す。
module ADDER4 (A, B, S, CO);
input [3:0] A, B;
output [3:0] S;
output CO;
wire [2:0] C;
HALF_ADDER U0 (.A(A[0]), .B(B[0]), .S(S[0]), .CO(C[0]));
FULL_ADDER U1 (.A(A[1]), .B(B[1]), .S(S[1]), .CIN(C[0]), .CO(C[1]));
FULL_ADDER U2 (.A(A[2]), .B(B[2]), .S(S[2]), .CIN(C[1]), .CO(C[2]));
FULL_ADDER U3 (.A(A[3]), .B(B[3]), .S(S[3]), .CIN(C[2]), .CO(CO));
endmodule
|
ここで注意して欲しいのは、モジュールの名前は識別子であり、テキスト 6-3 ページ左のルールに従って名付ける必要がある。例えば "4BIT_ADDER" のように、モジュール名の先頭一字を数字にすることはルール違反であり、許されない。(先頭一字に数字を許すプログラミング言語は多くない。このような名付けには違和感を感じるようになって欲しい。)
検証用モジュールの記述例を以下に示す。
`timescale 10ps / 10ps
module TESTBENCH;
reg [3:0] A, B;
wire [3:0] S;
wire CO;
ADDER4 CUT (.A(A), .B(B), .S(S), .CO(CO));
initial begin
$dumpfile("ADDER4.vcd");
$dumpvars(1, TESTBENCH);
A <= 4'b0000; B <= 4'b0000; #50 // S = 0000, CO = 0
A <= 4'b0011; B <= 4'b0000; #50 // S = 0011, CO = 0
A <= 4'b0110; B <= 4'b0010; #50 // S = 1000, CO = 0
A <= 4'b0011; B <= 4'b1011; #50 // S = 1110, CO = 0
A <= 4'b0111; B <= 4'b0111; #50 // S = 1110, CO = 0
A <= 4'b1000; B <= 4'b0110; #50 // S = 1110, CO = 0
A <= 4'b0110; B <= 4'b1011; #50 // S = 0001, CO = 1
A <= 4'b1101; B <= 4'b0111; #50 // S = 0100, CO = 1
A <= 4'b1010; B <= 4'b1110; #50 // S = 1000, CO = 1
$finish;
end
endmodule
|
検証用モジュール作成について、よく「全ての入力を試さなければならないか?」という質問を受ける。本課題では作成したモジュールが4ビット加算器であることが確認できる程度に選んで試せばよいものとしている。一般に大きなシステムを設計したとき、全ての状態で、全ての入力を試すことは不可能である。よって、一部の状態、入力のみで検証を行う他ない。ただし、コストや時間が許す限り、なるべく多くの状態、入力で検証を行うべきである。一般にバグの発見は遅ければ遅いほど、そのバグの修正にかかるコストは指数的に増える。
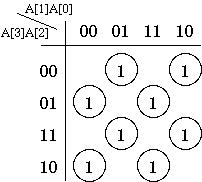
パリティチェッカのカルノー図を図1に示す。

|
| 図1. パリティチェッカのカルノー図 |
このカルノー図から得られる記述例を以下に示す。
module PARITY (A, E);
input [3:0] A;
output E;
assign E = (~A[3] & ~A[2] & ~A[1] & A[0])
|| (~A[3] & ~A[2] & A[1] & ~A[0])
|| (~A[3] & A[2] & ~A[1] & ~A[0])
|| (~A[3] & A[2] & A[1] & A[0])
|| ( A[3] & A[2] & ~A[1] & A[0])
|| ( A[3] & A[2] & A[1] & ~A[0])
|| ( A[3] & ~A[2] & ~A[1] & ~A[0])
|| ( A[3] & ~A[2] & A[1] & A[0]);
endmodule
|
上記記述でも誤りではないが、以下のように排他的論理和 (XOR) 演算子 ^ を用いて記述することが多い。カルノー図は与えられた真理値表から積和演算形の最簡形を得るのに有用である。しかし、一般的に良好な記述・回路構成を与えるものではない。
module PARITY (A, E);
input [3:0] A;
output E;
assign E = A[3] ^ A[2] ^ A[1] ^ A[0];
endmodule
|
検証用モジュールの記述例を以下に示す。
`timescale 10ps / 10ps
module TESTBENCH;
reg [3:0] A;
wire E;
PARITY CUT (.A(A), .E(E));
initial begin
$dumpfile("PARITY.vcd");
$dumpvars(1, TESTBENCH);
A <= 4'b0000; #50
A <= 4'b0001; #50
A <= 4'b0010; #50
A <= 4'b0011; #50
A <= 4'b0100; #50
A <= 4'b0101; #50
A <= 4'b0110; #50
A <= 4'b0111; #50
A <= 4'b1000; #50
A <= 4'b1001; #50
A <= 4'b1010; #50
A <= 4'b1011; #50
A <= 4'b1100; #50
A <= 4'b1101; #50
A <= 4'b1110; #50
A <= 4'b1111; #50
$finish;
end
endmodule
|
難波 一輝 (助教・伊藤・北神・難波研究室)
工学部1号棟4階409号室、内線3255、043-290-3255、namba@ieee.org