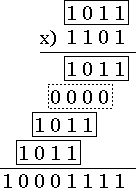
2進数表記した2値に対する筆算による乗算例を図1に示す。

|
| 図1. 乗算例 |
例の場合は、乗数の第3, 2, 0 ビットが 1、第1ビットが 0 であり、被乗数1011 を 3, 2, 0 ビット左シフトして得られる3値の和を取ることにより積を得ることができる。一般に、乗数の各ビットの値を調べ、1となるすべてのビット(第iビットとする)について、被乗数をiビット左シフトして得られる値を求め、それぞれの和を取ることにより、積を得ることができる。
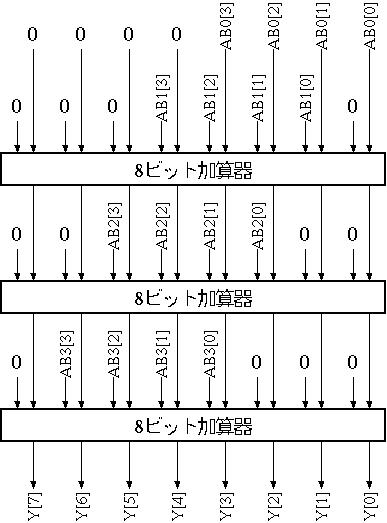
4ビット乗算器の作成例を図2 に示す。
|
| 図2. 4ビット乗算器 |
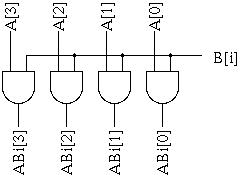
ここで、ABi (i=0〜3) は B[i] が 1 のときバスAと等しい値、0 のとき全零となるバスであり、図3 に示すようにバスAの各値と B[i] の論理積(AND)演算により得ることができる。
|
| 図3. ABi (i=0〜3) を求める回路 |
積Yは値ABi (i=0〜3) をiビット左シフトして得られる値の総和をとることにより得られる。左シフト操作には特殊な回路を用いる必要はなく、配線を左にずらすことで実現できる。積Yは8ビット値で得られる。一般に積の桁数は、高々、被乗数と乗数の桁数の和である。この場合は被乗数と乗数の桁数は共に高々4桁であり、積の桁数も高々4+4=8桁となる。
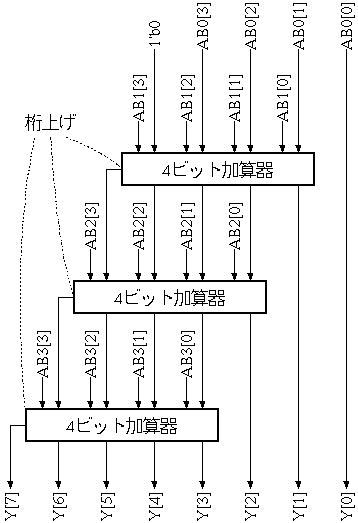
図2 に示す乗算器から冗長な箇所(入力が0である箇所等)を削除した4ビット乗算器を図4に示す。一般に乗算を行う場合、被乗数の桁数と同じビット数の加算器(この場合は4ビット加算器)を用意すればよい。
|
| 図4. 回路量を減らした4ビット乗算器 |
図4に基づいて作成した4ビット乗算器を以下に示す。モジュール ADDER4 は課題3 で作成した4ビット加算器である。また、モジュール MULTIPLIER4X1 は図3に示した ABi を求める回路である。
module MULTIPLIER4X4(A, B, Y);
input [3:0] A, B;
output [7:0] Y;
wire [3:0] AB3, AB2, AB1, AB0;
wire [3:0] AB10, AB210;
wire CO10, CO210;
MULTIPLIER4X1 U0 (.A(A), .B(B[0]), .Y(AB0));
MULTIPLIER4X1 U1 (.A(A), .B(B[1]), .Y(AB1));
MULTIPLIER4X1 U2 (.A(A), .B(B[2]), .Y(AB2));
MULTIPLIER4X1 U3 (.A(A), .B(B[3]), .Y(AB3));
assign Y[0] = AB0[0];
ADDER4 U4 (.A({ 1'b0, AB0[3], AB0[2], AB0[1]}),
.B({ AB1[3], AB1[2], AB1[1], AB1[0]}),
.S(AB10), .CO(CO10));
assign Y[1] = AB10[0];
ADDER4 U5 (.A({ CO10, AB10[3], AB10[2], AB10[1]}),
.B({ AB2[3], AB2[2], AB2[1], AB2[0]}),
.S(AB210), .CO(CO210));
assign Y[2] = AB210[0];
ADDER4 U6 (.A({ CO210, AB210[3], AB210[2], AB210[1]}),
.B({AB3[3], AB3[2], AB3[1], AB3[0]}),
.S({ Y[6], Y[5], Y[4], Y[3]}),
.CO(Y[7]));
endmodule
module MULTIPLIER4X1(A, B, Y); // 図3に示した ABi を求める回路
input [3:0] A;
input B;
output [3:0] Y;
assign Y[3] = A[3] & B;
assign Y[2] = A[2] & B;
assign Y[1] = A[1] & B;
assign Y[0] = A[0] & B;
endmodule
|
ここで 1'b0 は 1ビットの信号値(定数値) 0を意味する。一般にn'bxxx...x は、値がxxx...x(2進表記) なるnビットの信号値(定数値)を意味する。なお、単に xxx...x と値を書いたとき、10進表記された値と見なされる
この乗算器は加算器を3個持つ。一般に乗算器は加算器と比べ回路量がとても大きい。フリップフロップ等をうまく用いることにより、回路量を減らす方法もあるが、この場合は演算に時間がかかる。このような事情から、COMET II のように、乗算器、乗算命令を持たないプロセッサもある。
加算は+演算子により記述できる。この場合、設計者がわざわざ加算器の構成を記述しなくとも、論理合成ツールが加算器を作成してくれる。以下に+演算子を用いた乗算器の構成を示す。
module MULTIPLIER4X4(A, B, Y);
input [3:0] A, B;
output [7:0] Y;
wire [3:0] AB3, AB2, AB1, AB0;
wire [4:0] AB10, AB210;
assign AB0 = A & {4{B[0]}};
/* {4{B[0]}} は {B[0], B[0], B[0], B[0]} なる 4ビットバス */
assign AB1 = A & {4{B[1]}};
assign AB2 = A & {4{B[2]}};
assign AB3 = A & {4{B[3]}};
assign Y[0] = AB0[0];
assign AB10 = {1'b0, AB0[3:1]} + AB1;
/* AB0[3:1] は {AB0[3], AB0[2], AB0[1]} なるバス */
/* 4ビットバス同士の加算結果は5ビットバスで得られる */
/* 最上位ビット(AB10[4]) は桁上げ、 */
/* 残る4ビット(AB10[3:0]) は和である */
assign Y[1] = AB10[0];
assign AB210 = AB10[4:1] + AB2;
assign Y[2] = AB210[0];
assign Y[7:3] = AB210[4:1] + AB3;
endmodule
|
加算(+)だけでなく、減算(-)、乗算(*)、除算(/)、バレルシフト(>>, <<) 等の演算子も用いることができる。ただ、これら演算子を用いた回路を論理合成するためには、各演算子用のライブラリを持っている、つまり、論理合成ツールが各演算回路の構成を知っている必要がある。ライブラリを持っていない場合は、論理合成するために、これらの演算子を用いずに回路記述する必要がある。
難波 一輝 (助教・伊藤・北神・難波研究室)
工学部1号棟4階409号室、内線3255、043-290-3255、namba@ieee.org